Question

A body of mass 400 g is moving along a smooth surface at a velocity of 1.25 m/s towards the east. It strikes a body of mass 600 g, initially at rest. The 400 g mass then moves at a velocity of 1.00 m/s in a direction 36.9? north of east. (a) what is the easterly component of the total momentum of the system before and after the collision? (b) What is the northerly component of the total momentum of the system before and after the collision? (c) Determine the final velocity of the 600 g body.

Answer 1

(a) 0.5 kg m/s

Before the collision, only the first body is moving, so only the first body contributes to the total momentum.

The first body has

m = 400 g = 0.4 kg (mass)

v = 1.25 m/s (velocity, towards east direction)

So its momentum is

`p_x=mv = (0.4 kg)(1.25 m/s)=0.5 kg m/s`

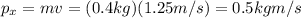
And since the body is moving along the east direction, this is also the easterly component of the total momentum before the collision.

(b) Zero

Before the collision, we have:

- The first body moving along the east direction --> so its northerly component is zero

- The second body at rest --> this means that it does not contribute to the momentum, since it is zero

This means that the northerly component of the total momentum before the collision is zero.

(c) 0.5 m/s at 53.1 degrees south of east

The law of conservation of momentum states that each component of the total momentum must be conserved.

- Along the easterly direction:

`p_x = p_(1x) + p_(2x)`

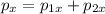
where

`p_x = 0.5 kg m/s` is the easterly component of the total momentum

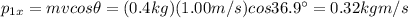`p_(1x) = m v cos \theta = (0.4 kg)(1.00 m/s) cos 36.9^(\circ) =0.32 kg m/s` is the easterly component of the momentum of the first body after the collision

`p_(2x)` is the easterly component of the momentum of the second body (mass m = 600 g = 0.6 kg) after the collision

Solving the equation we find

`p_(2x) = p_x - p_(1x) = 0.5 kg m/s - 0.32 kg m/s = 0.18 kg m/s`

- Along the northerly direction:

`p_y = p_(1y) + p_(2y)`

where

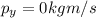`p_y = 0 kg m/s` is the northerly component of the total momentum

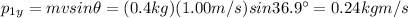`p_(1y) = m v sin \theta = (0.4 kg)(1.00 m/s) sin 36.9^(\circ) =0.24 kg m/s` is the northerly component of the momentum of the first body after the collision

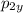`p_(2y)` is the northerly component of the momentum of the second body (mass m = 600 g = 0.6 kg) after the collision

Solving the equation we find

`p_(2y) = p_y - p_(1y) = 0 - 0.24 kg m/s = -0.24 kg m/s`

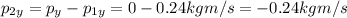
So now we find the momentum of the 600 g body after the collision:

`p_2=\sqrt{p_(2x)^2 + p_(2y)^2}=√((0.18)^2+(-0.24)^2)=0.3 kg m/s`

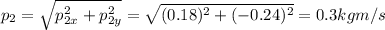
and so its final speed is

`v=(p_2)/(m)=(0.3 kg m/s)/(0.6 kg)=0.5 m/s`

and the direction is

`\theta=tan^(-1) ((p_(2y))/(p_(2x)))=tan^(-1) ((-0.24)/(0.18))=-53.1^(\circ)`

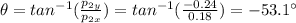
so 53.1 degrees in the south-east direction.