(a) 1200 rad/s
The angular acceleration of the rotor is given by:
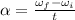
where we have
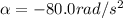 is the angular acceleration (negative since the rotor is slowing down)
is the angular acceleration (negative since the rotor is slowing down)
 is the final angular speed
is the final angular speed
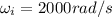 is the initial angular speed
is the initial angular speed
t = 10.0 s is the time interval
Solving for
 , we find the final angular speed after 10.0 s:
, we find the final angular speed after 10.0 s:
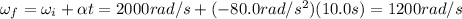
(b) 25 s
We can calculate the time needed for the rotor to come to rest, by using again the same formula:
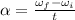
If we re-arrange it for t, we get:
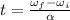
where here we have
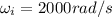 is the initial angular speed
is the initial angular speed
 is the final angular speed
is the final angular speed
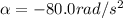 is the angular acceleration
is the angular acceleration
Solving the equation,
