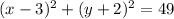Question

The equation of the circle with center (3, -2) and radius 7 is:

Answer 1

`(x-3)^2 + (y+2)^2 = 49`

Explanation:

The general equation of a circle has the following form:

`(x-h)^2 + (y-k)^2 = r^2`

Where the point (h, k) represents the center of the circle and r represents the radius

In this case we know that the center is (3, -2) and the radius is 7.

Therefore:

`h=3\\k = -2\\r=7`

Finally the equation of the circle is:

`(x-3)^2 + (y-(-2))^2 = 7^2`

`(x-3)^2 + (y+2)^2 = 49`

Answer 2

`(x-3)^(2)+(y+2)^(2)=49`

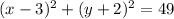
Explanation:

The center-radius form of the equation of a circle is in the format;

`(x-h)^(2)+(y-k)^(2)=r^(2)`

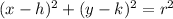
with the center being at the point (h, k) and the radius being r units.

We simply plugin the values of the center and radius given in order to determine the equation of the circle;

The equation of the circle with center (3, -2) and radius 7 is;

`(x-3)^(2)+(y+2)^(2)=49`