Question

Which statement regarding the function y=sin(x) is true?

a. Reflection over the y-axis will not change the graph since sine is an even function
b. Sin(x)=sin(-x)
c. Reflection over either the x-axis or y-axis will change the graph
d. Sin(x)=-sin(x)

Answer 1

c. Reflection over either the x-axis or y-axis will change the graph

Explanation:

a. Reflection over the y-axis will not change the graph since sine is an even function.

This is false because
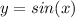`y=sin(x)` is an odd function, not an even one. This means that
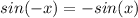`sin(-x)=-sin(x)`, and a reflection over the y-axis will change the graph.

b. Sin(x)=sin(-x)

This is false because we said that
`sin(-x)=-sin(x)`

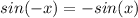
c. Reflection over either the x-axis or y-axis will change the graph

This is true. Since
`sin(x)` is an odd function, then reflection over either the x-axis or y-axis will change the graph as we said in a. So, for
`f(x)`:

REFLEXION IN THE X-AXIS:

`h(x)=-f(x)`

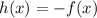
REFLEXION IN THE Y-AXIS:

`h(x)=f(-x)`

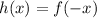
d. Sin(x)=-sin(x)

False by the same explanation as b.