Question

you begin playing a new game called hooville. You are King of Hooville, a city of owls that is located in the treetops near Fords of Beruna. In order to know how much food to produce each year, you must predict the population of Hooville. History shows that the population growth rate of Hooville is 3.5%. The current population of owls is 80,000. Using the monetary growth formula that you used in the Uncle Harold problem, write a new function for the population of hooville. (let n=1.)​ PLEASE HELP. I HAVE NO IDEA WHAT IM DOING!!

Answer 1

Part 1)
`y=80,000(1.035)^(x)`

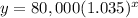
Part 2) The table in the attached figure

Part 3) The graph in the attached figure

Explanation:

Part 1) Find the population function

In this problem we have a exponential function of the form

`y=a(b)^(x)`

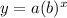
where

y ----> is the population

x ----> the time in years

a is the initial value (a=80,000 people)

b is the base (b=100%+3.5%=103.5%=1.035)

substitute

`y=80,000(1.035)^(x)`

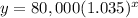
Part 2) Construct the table

For x=0 years

substitute in the function equation

`y=80,000(1.035)^(0)=80,000\ people`

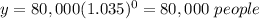
For x=10 years

substitute in the function equation

`y=80,000(1.035)^(10)=112.848\ people`

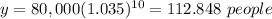
For x=20 years

substitute in the function equation

`y=80,000(1.035)^(20)=159,183\ people`

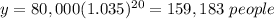
For x=40 years

substitute in the function equation

`y=80,000(1.035)^(40)=316,741\ people`

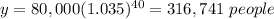
For x=50 years

substitute in the function equation

`y=80,000(1.035)^(50)=446,794\ people`

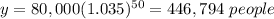
For x=75 years

substitute in the function equation

`y=80,000(1.035)^(75)=1,055,884\ people`

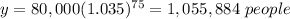
For x=100 years

substitute in the function equation

`y=80,000(1.035)^(100)=2,495,313\ people`

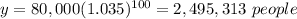
Part 3) The graph in the attached figure