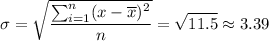Question

Find the standard deviation of 21, 31, 26, 24, 28, 26

Answer 1

Given the dataset

`x = \{21,\ 31,\ 26,\ 24,\ 28,\ 26\}`

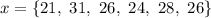
We start by computing the average:

`\overline{x} = (21+31+26+24+28+26)/(6)=(156)/(6)=26`

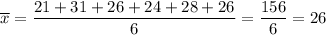
We compute the difference bewteen each element and the average:

`x-\overline{x} = \{-6,\ 5,\ 0,\ -2,\ 2,\ 0\}`

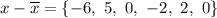
We square those differences:

`(x-\overline{x})^2 = \{36,\ 25,\ 0,\ 4,\ 4,\ 0\}`

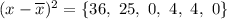
And take the average of those squared differences: we sum them

`\displaystyle \sum_(i=1)^n (x-\overline{x})^2=36+25+4+4+0+0=69`

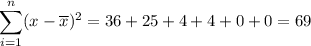
And we divide by the number of elements:

`\displaystyle \sigma^2=\frac{\sum_(i=1)^n (x-\overline{x})^2}{n} = (69)/(6) = 11.5`

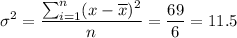
Finally, we take the square root of this quantity and we have the standard deviation:

`\displaystyle\sigma = \sqrt{\frac{\sum_(i=1)^n (x-\overline{x})^2}{n}} = √(11.5)\approx 3.39`