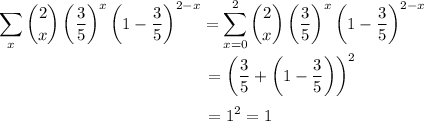Question

A box contains 3 red balls and 2 green balls. Two balls are selected at random with replacement. Find the probability distribution of the random variable X that measures the number of red balls selected and show that it is legitimate probability mass function.

Answer 1

The probability of drawing a red ball is

`(\dbinom 31 \dbinom 20)/(\dbinom 51) = \frac35`

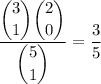
Since we are replacing each ball as it's drawn, this probability stays the same. So
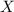`X` follows a binomial distribution with
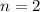`n=2` draws and success probability
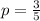`p=\frac35`, and so

`\mathrm{Pr}(X = x) = \begin{cases} \dbinom2x \left(\frac35\right)^x \left(1 - \frac35\right)^(2 - x) & \text{if } x \in\{0,1,2\} \\\\ 0 & \text{otherwise}\end{cases}`

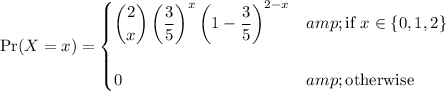
This is a valid PMF, since by the binomial theorem,

`\displaystyle \sum_x \binom 2x \left(\frac35\right)^x \left(1 - \frac35\right)^(2-x) = \sum_(x=0)^2 \binom 2x \left(\frac35\right)^x \left(1 - \frac35\right)^(2-x) \\\\ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~= \left(\frac35 + \left(1 - \frac35\right)\right)^2 \\\\ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ = 1^2 = 1`