Question

At a competition with 7 runners, medals are awarded for first, second, and

third places. Each of the 3 medals is different. How many ways are there to
award the medals?
Decide if this is a permutation or a combination, and find the number of ways
to award the medals.
O
A. Permutation; number of ways = 210
O
B. Combination; number of ways = 210
O
c. Permutation; number of ways = 35
O
D. Combination; number of ways = 35

Answer 1

210

Explanation:

Answer 2

Option A - Permutation; number of ways = 210

Explanation:

Given : At a competition with 7 runners, medals are awarded for first, second, and third places. Each of the 3 medals is different.

To find : How many ways are there to award the medals?

Solution :

There are 7 runners but medals are three.

The first runner up got first medal as one is locked.

The second runner up got second medal as second is locked.

The third runner up got the third medal.

So, There is a permutation.

Number of ways to award the medals is
`^7P_3`

We know,
`^nP_r=(n!)/((n-r)!)`

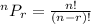
Substitute the values,

`^7P_3=(7!)/((7-3)!)`

`^7P_3=(7* 6* 5* 4!)/(4!)`

`^7P_3=210`

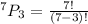
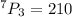
Therefore, Option A is correct.

Permutation; number of ways = 210