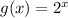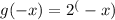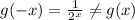Answer: Second Option
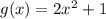
Explanation:
By definition, a function f(x) is an even function if:
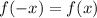
This means that each input value x and its negative -x are assigned the same output value y.
To verify which of the functions is even, you must test
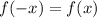 for each of them
for each of them
First option
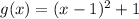
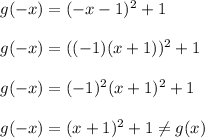
Second option
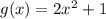
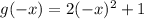
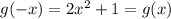
Third option
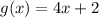
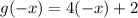
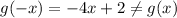
Fourth option