Answer:
D (1,0)
Explanation:
Let the coordinates of D be (a,b).
The diagonals of a parallelogram bisect each other.
The midpoint of AC should be the same as the midpoint of BD.
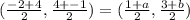
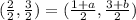
Compare corresponding coordinates
This implies that:
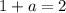 ,
,
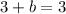
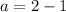 ,
,
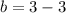
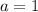 ,
,
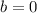
Therefore the coordinates of D are: (1,0)