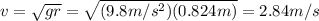Question

a 2.35 water bucket is swung in a full cirlce of radius 0.824 m just fast enough so that the water doesn't fall out the top meaning n equals zero there. What is the speed of the water at the top

Answer 1

2.84 m/s

Step-by-step explanation:

At the top position of the circular trajectory, the normal reaction is zero:

N = 0

So it means that the only force that is providing the centripetal force is the gravitational force (the weight of the bucket). Therefore we have:

`mg = m (v^2)/(r)`

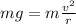
where

m is the mass of the water bucket

g = 9.8 m/s^2 is the acceleration of gravity

v is the speed of the bucket

r = 0.824 m is the radius of the circle

Solving for v,

`v=√(gr)=√((9.8 m/s^2)(0.824 m))=2.84 m/s`