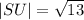Question

A parallelogram whose vertices have coordinates R(1, -1), S(6, 1), T(8, 5), and U(3, 3) has a shorter diagonal of ___ . 5 √(13) √(97)

Answer 1

`|SU|=√(13)`

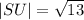
Explanation:

The given parallelogram has vertices R(1, -1), S(6, 1), T(8, 5), and U(3, 3) .

Recall the distance formula;

We use the distance formula to determine the length of the diagonals.

For diagonal R(1,-1) and T(8,5), We have;

`|RT|=√((8-1)^2+(5--1)^2)`

`|RT|=√((7)^2+(6)^2)`

`|RT|=√(49+36)`

`|RT|=√(85)`

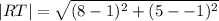
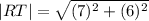
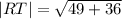
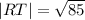
For the diagonal S(6,1) U(3,3)

`|SU|=√((6-3)^2+(5-3)^2)`

`|SU|=√((3)^2+(2)^2)`

`|SU|=√(9+4)`

`|SU|=√(13)`

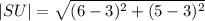
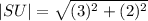
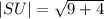
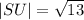
Therefore the shorter diagonal is:

`|SU|=√(13)`