Question

Consider the quadratic function f(x) = 2x2 – 8x – 10. The x-component of the vertex is . The y-component of the vertex is . The discriminant is b2 – 4ac = (–8)2 – (4)(2)(–10) = .

Answer 1

Consider the quadratic function f(x) = 2x2 – 8x – 10.

The x-component of the vertex is

✔ 2

The y-component of the vertex is

✔ –18

The discriminant is b2 – 4ac = (–8)2 – (4)(2)(–10) =

✔ 144

Answer 2

Part 1) The x-component of the vertex is 2 and the y-component of the vertex is -18

Part 2) The discriminant is 144

Explanation:

we have

`f(x)=2x^(2)-8x-10`

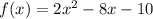
step 1

Find the discriminant

The discriminant of a quadratic equation is equal to

`D=b^(2)-4ac`

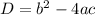
in this problem we have

`f(x)=2x^(2)-8x-10`

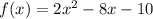
so

`a=2\\b=-8\\c=-10`

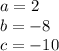
substitute

`D=(-8)^(2)-4(2)(-10)`

`D=64+80=144`

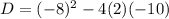
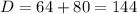
The discriminant is greater than zero, therefore the quadratic equation has two real solutions

step 2

Find the vertex

Convert the quadratic equation into vertex form

`f(x)+10=2x^(2)-8x`

`f(x)+10=2(x^(2)-4x)`

`f(x)+10+8=2(x^(2)-4x+4)`

`f(x)+18=2(x-2)^(2)`

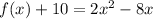
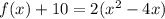
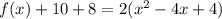
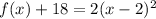
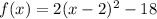`f(x)=2(x-2)^(2)-18` -----> equation in vertex form

The vertex is the point (2,-18)

therefore

The x-component of the vertex is 2

The y-component of the vertex is -18