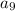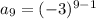Question

Find the 9th term of the following geometric sequence 1 -3 9 -27

Answer 1

Answer: The 9th term is 6561

Explanation:

The geometric sequences have the following formula

`a_n = a_1(r)^(n-1)`

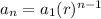
Where
`a_1` is the first term of the sequence and r is the common ratio between the consecutive terms of the sequence

In this case the sequence is 1 -3 9 -27

So
`a_1 = 1`

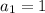
Observe that the common ratio r is:

`r=(-3)/(1)=(9)/(3)=(-27)/(9)=-3`

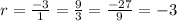
So the formula is:

`a_n = (-3)^(n-1)`

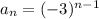
We want to find
`a_9`

`a_9 = (-3)^(9-1)`

`a_9 = (-3)^(8)=6561`