Question

D(5, 7), E(4, 3), and F(8, 2) form the vertices of a triangle. What is m∠DEF? A. 30° B. 45° C. 60° D. 90°

Answer 1

The answer is D. 90*

Explanation:

I got it right on the Edmentum test.

Answer 2

Option D. 90°

Explanation:

we have

`D(5, 7),E(4, 3),F(8, 2)`

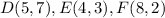
Plot the vertices

see the attached figure

the formula to calculate the distance between two points is equal to

`d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}`

step 1

Find the distance DE

`D(5, 7),E(4, 3)`

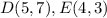
substitute

`d=\sqrt{(3-7)^(2)+(4-5)^(2)}`

`d=\sqrt{(-4)^(2)+(-1)^(2)}`

`DE=√(17)\ units`

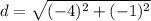
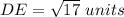
step 2

Find the distance EF

`E(4, 3),F(8, 2)`

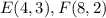
substitute

`d=\sqrt{(2-3)^(2)+(8-4)^(2)}`

`d=\sqrt{(-1)^(2)+(4)^(2)}`

`EF=√(17)\ units`

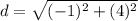
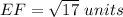
step 3

Find the distance DF

`D(5, 7),F(8, 2)`

substitute

`d=\sqrt{(2-7)^(2)+(8-5)^(2)}`

`d=\sqrt{(-5)^(2)+(3)^(2)}`

`DF=√(34)\ units`

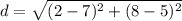
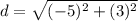
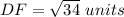
step 4

The triangle DEF is a right triangle because satisfy the Pythagoras theorem

so

`(√(34))^(2)=(√(17))^(2)+(√(17))^(2)`

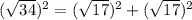
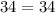`34=34` -----> is true

therefore

The measure of angle DEF is a right angle