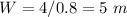Question

The perimeter of the original rectangle on the left is 30 meters. The perimeter of the reduced rectangle on the right is 24

meters.
8 m
Not drawn to scale
What is x, the width of the original rectangle on the left? Round to the nearest hundredth if necessary.
5 meters
8 meters
10 meters
12 meters

Answer 1

A. 5 meters

Explanation:

Answer 2

5 meters

Explanation:

step 1

Find the scale factor

we know that

If two figures are similar, then the ratio of its perimeters is equal to the scale factor

Let

z -----> the scale factor

P1 -----> the perimeter of the reduced rectangle on the right

P2 ----> the perimeter of the original rectangle on the left

`z=(P1)/(P2)`

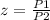
substitute

`z=(24)/(30)=0.8`

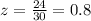
step 2

Find the width of the reduced rectangle on the right

`P1=2(L+W)`

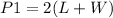
substitute the given values

we have

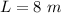`L=8\ m` ---> see the attached figure to better understand the problem

`24=2(8+W)`

`12=8+W`

`W=4\ m`

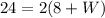
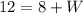
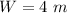
step 3

Find the width of the original rectangle on the left

To find the width of the original rectangle on the left, divide the width of the reduced rectangle on the right by the scale factor

so

`W=4/0.8=5\ m`