Question

Select the correct answer.

Which point lies on a circle with a radius of 5 units and center at P(6, 1)?

A.
Q(1, 11)
B.
R(2, 4)
C.
S(4, -4)
D.
T(9, -2)
Reset Next

Answer 1

B.

Explanation:

The general equation of a circle is
`(x-h)^(2)+(y-k)^(2) = r^(2)` where (h,k) is the center and r the radius. In this case, the general equation of the circle with radius 5 and center at (6,1) is
`(x-6)^(2)+(y-1)^(2) = 5^(2)`, so the point that satisfies the equation will be in the circle.

A.
`(1-6)^(2)+(11-1)^(2) = 25+100 = 125` this option is not correct.

B.
`(2-6)^(2)+(4-1)^(2) = 16+9= 25` this option is correct so is the answer.

Answer 2

Option B R(2,4) is correct

Explanation:

The equation of the circle is:

`(x-a)^2 + (y-b)^2 = r^2`

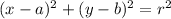
Where r = radius

a and b are coordinates of the center of circle.

To check which point lies on a circle, we need to verify the equation

`(x-6)^2 + (y-1)^2 = (5)^2`

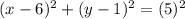
We will check for each option.

Option A Q(1,11)

x=1 and y =11

`(1-6)^2 + (11-1)^2 = 25\\(-5)^2 + (10)^2 = 25\\25 + 100 = 25\\125 \\eq 25`

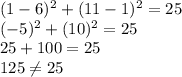
So, Option A is incorrect

Option B R(2,4)

x =2 and y = 4

`(2-6)^2 + (4-1)^2 = 25\\(-4)^2 + (3)^2 = 25\\16 + 9 = 25\\25 = 25`

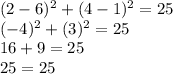
Option B is correct.

Option C S(4,-4)

x =4 and y =-4

`(4-6)^2 + (-4-1)^2 = 25\\(-2)^2 + (-5)^2 = 25\\4 + 25 = 25\\29 \\eq 25`

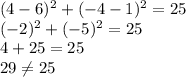
Option C is incorrect

Option D T(9,-2)

x =9 and y =-2

`(9-6)^2 + (-2-1)^2 = 25\\(3)^2 + (-3)^2 = 25\\9 + 9 = 25\\18 \\eq 25`

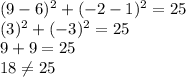
Option D is incorrect.