Answer:
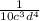
Explanation:
THE GIVEN EXPRESSION IS
![\sqrt[3]{(1)/(1000c^(9)d^(12) ) }](https://img.qammunity.org/2020/formulas/mathematics/high-school/59ujfpcxg2uxjmcumkxncpfcn9kpmo4nbx.png)
To simplify this expression, we just have to apply the cubic root to each part of the fraction, as follows
![\frac{\sqrt[3]{1} }{\sqrt[3]{1000c^(9) d^(12) } }](https://img.qammunity.org/2020/formulas/mathematics/high-school/wd5dgony80ztn7fw61kfuebmwbhbi9v92o.png)
Then, we solve each root. Remember that to solve roots of powers, we just need to divide the exponent of the power by the index of the root, as follows
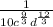
Therefore, the equivalent expression is
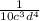
So, the right answer is the third choice.