Answer:
A). (2, -1)
B). Average rate of change of function A = 1
C). Average rate of change of function B = 1.5
D). Graph of function B increases faster than function A.
Explanation:
A). vertex of the function A will be (2, -1)
and vertex of the function B will be same as function A, (2, -1)
B). Average rate of change in function A between x = 2 and x = 3 will be
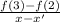
Equation of the function A will be f(x) = (x - 2)²-(-1)
f(x) = (x - 2)² + 1
f(3) = (3 -2)² + 1
= 1² + 1 = 2
f(2) = 0 + 1 = 1
Therefore, rate of change =
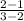 =1
=1
C). Average rate of change of function B will be
=
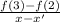
=
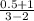 [ from the given table]
[ from the given table]
= 1.5
D).Since rate of change of graph B is greater than graph A therefore, function B will increase faster than function A.