Answer:
3
Step-by-step explanation:
The half-life of a radioactive isotope is the time it takes for the mass of the sample to halve.
This can be rewritten as follows:

where
m(t) is the mass of the sample at time t
m0 is the original mass of the sample
n is the number of half-lives that passed
We see that if we take n=3, the amount of original sample left is
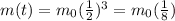
So 3 (3 half-lives) is the correct answer.