Question

Given that triangle PHT is a right triangle and Line HY is an altitude, what is the missing justification in the proof that (PH)^2 + (HT)^2 = (PT)^2?

Answer 1

The correct option is D.

Explanation:

Given information: Triangle PHT is a right triangle and Line HY is an altitude.

According to the reflexive property, a side or an angle is congruent to itself.

If A is an angle of a triangle then using reflexive property

`\angle A\cong \angle A`

`\angle PHT\cong \angle HYT` (Both are right angles)

`\angle T\cong \angle T` (Reflexive property)

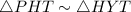`\triangle PHT\sim \triangle HYT` (AA rule of similarity)

Other statements and reasons are present in the table.

The missing reason is reflexive property. Therefore the correct option is D.

Answer 2

Answer: the answer is D

Explanation: