Answer:
1. x=±4
2. t=±9
3. r=±10
4. x=±12
5. s=±5
Explanation:
1. x^2 = 16
Taking square root on both sides
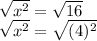
x=±4
2. t^2=81
Taking square root on both sides
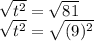
t=±9
3. r^2-100=0

r=±10
4. x²-144=0
x²=144
Taking square root on both sides
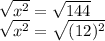
x=±12
5. 2s²=50
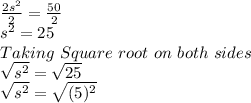
s=±5 ..