Question

Use your calculator to evaluate the limit from x equals 0 to 2 of the sine of x squared, dx. Give your answer to the nearest integer.

Answer 1

`\int_(0)^(2)sin(x^(2))dx \approx 1units^2`

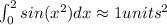
Explanation:

First of all, the graph of the function
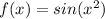`f(x)=sin(x^2)` is shown in the first figure below. We need to calculate the area under the curve which is in fact the definite integral. From calculus, we know that
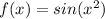`f(x)=sin(x^2)` is non integrable, that is, it doesn't have a primitive, so we must use calculator to evaluate
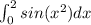`\int_(0)^(2)sin(x^(2))dx`. To do so, calculator uses the Taylor Series, so:

`sin(x^(2))=\sum_(n=-\infty)^(+\infty)((-1)^(n))/((2n+1)!)x^(4n+2)$`

You an use a calculator or any program online, and the result will be:

`\int_(0)^(2)sin(x^(2))dx=0.804units^2`

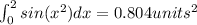
Since the problem asks for rounding the result to the nearest integer, then we have:

`\boxed{\int_(0)^(2)sin(x^(2))dx \approx 1units^2}`

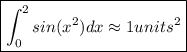
The area is the one in yellow in the second figure.