Answer:
The function is:

Explanation:
Note that the number of people increases by a factor of 1.5 per hour, and the initial number of people is 68.
So:
After an hour the number of people is:
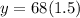
After two hours the number of people is:

After x hours the number of people is:

Therefore, the exponential growth function that models the number of people y at the fair after x hours is:
