Question

HELP ME MATH

Match each quadratic function to its graph.

Answer 1

Answer with explanation:

We know that the general equation of a parabola in vertex form is given by:

`y=a(x-h)^2+k`

where the vertex of the parabola is at (h,k)

and if a>0 then the parabola is open upward and if a<0 then the parabola is open downward.

a)

`f(x)=-2(x+3)^2-1`

Since, the leading coefficient is negative.

Hence, the graph of the function is a parabola which is downward open.

The vertex of the function is at (-3,-1)

b)

`f(x)=-2(x+3)^2+1`

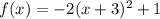
Again the leading coefficient is negative.

Hence, graph is open downward.

The vertex of the function is at (-3,1)

c)

`f(x)=2(x+3)^2+1`

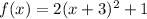
The leading coefficient is positive.

Hence, graph is open upward.

The vertex of the function is at (-3,1)

d)

`f(x)=2(x-3)^2+1`

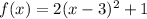
The leading coefficient is positive.

Hence, graph is open upward.

The vertex of the function is at (3,1)

Answer 2

See the attached picture.

The negative sign in front of the 2 makes the graph an upside down U shape.