Question

Consider a sample with data values of 27, 24, 23, 15, 30, 36, 29, and 24. Compute the range, interquartile range, variance, and standard deviation (to a maximum of 2 decimals, if decimals are necessary. Use Excel's =quartile.exc function).

Answer 1

The range is 21

The interquartile range is 6

The variance is 33

The standard deviation (σ) is 5.74

Explanation:

* Lets study the information to solve the problem

- The values of the data are 27 , 24 , 23 , 15 , 30 , 36 , 29 , 24

- They are eight values

* lets arrange them from small to big

∴ The values are 15 , 23 , 24 , 24 , 27 , 29 , 30 , 36

* Now lets solve the problem

# The range

- It is the difference between the largest and the smallest values

∵ The largest value is 36

∵ The smallest value is 15

∴ The range = 36 - 15 = 21

* The range is 21

# The interquartile range

- The steps to find the interquartile range is:

1- Arrange the values from the smallest to the largest

∴ The values are 15 , 23 , 24 , 24 , 27 , 29 , 30 , 36

2- Find the median

- The median is the middle value after arrange them

* If there are two values in the middle take their average

∵ The values are 8 then the 4th and the 5th are the values

∵ The 4th is 24 and the 5th is 27

∴ The median =
`(24+27)/(2)=(51)/(2)=25.5`

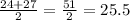
∴ The median is 25.5

3- Calculate the median of the lower quartile

- The lower quartile is the median of the first half data values

∵ There are 8 values

∴ The first half is the first four values

∴ The first half values are 15 , 23 , 24 , 24

∵ The middle values are 23 and 24

∴ The median of lower quartile =
`(23+24)/(2)=(47)/(2)= 23.5`

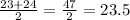
- Similar find the median of the upper quartile

- The upper quartile is the median of the second half data values

∵ There are 8 numbers

∴ The second half is the last four values

∴ The second half values are 27 , 29 , 30 , 36

∵ The middle values are 29 and 30

∴ The median of upper quartile =
`(29+30)/(2)=(59)/(2)=29.5`

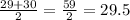
4- The interquartile range (IQR) is the difference between the upper

and the lower medians

∴ The interquartile range = 29.5 - 23.5 = 6

* The interquartile range is 6

# The variance

- The variance is the measure of how much values in a set of data are

likely to differ from the mean value of the same data

- The steps to find the variance

1- Find the mean of the data

∵ The mean = sum of the data ÷ the number of the values

∵ The sum = 15 + 23 + 24 + 24 + 27 + 29 + 30 + 36 = 208

∵ The number of values is 8

∴ The mean =
`(208)/(8)=26`

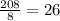
∴ The mean is 26

2- Subtract the mean from each value and square the answer

∴ 15 - 26 = -11 ⇒ (-11)² = 121

∴ 23 - 26 = -3 ⇒ (-3)² = 9

∴ 24 - 26 = -2 ⇒ (-2)² = 4

∴ 24 - 26 = -2 ⇒ (-2)² = 4

∴ 27 - 26 = 1 ⇒ (1)² = 1

∴ 29 - 26 = 3 ⇒ (3)² = 9

∴ 30 - 26 = 4 ⇒ (4)² = 16

∴ 36 - 26 = 10 ⇒ (10)² = 100

3- Add all of these squared answer and divide the sum by the number

of the values

∴ The sum = 121 + 9 + 4 + 4 + 1 + 9 + 16 + 100 = 264

∵ They are 8 values

∴ The variance (σ²) =
`(264)/(8)=33`

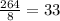
* The variance is 33

# The standard deviation

- It is the square root of the variance

∵ The variance = 33

∴ The standard deviation (σ) = √33 = 5.74

* The standard deviation (σ) is 5.74