Answer:
P' (−11, 13), Q' (−17, −19), R' (23, 27)
Explanation:
When we reflect a point across the x-axis, we negate the y-coordinates to obtain the image points.
The mapping for the reflection across the x-axis is
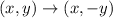
The vertices of the given figure are;
P(−11,−13), Q(−17,19), and R(23,−27)
We apply the rule to obtain:
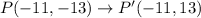

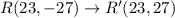
The correct option is P' (−11, 13), Q' (−17, −19), R' (23, 27)