Question

A reaction taking place in a container with a piston-cylinder assembly at constant temperature produces a gas, and the volume increases from 127 mL to 654 mL against an external pressure of 860 torr. Calculate the work done in Joules (J)

Answer 1

60.4 J

Step-by-step explanation:

The work done by the gas is given by:

`W=p(V_f-V_i)`

where

p is the gas pressure

`V_f` is the final volume of the gas

`V_i` is the initial volume

We must convert all the quantities into SI units:

`p=860 torr \cdot (1.013\cdot 10^5 pa)/(760 torr)=1.146\cdot 10^5 Pa`

`V_i = 127 mL = 0.127 L = 0.127 dm^3 = 0.127 \cdot 10^(-3)m^2`

`V_f = 654 mL = 0.654 L = 0.654 dm^3 = 0.654 \cdot 10^(-3)m^2`

So the work done is

`W=(1.146\cdot 10^5 Pa)(0.654\cdot 10^(-3) m^3-0.127\cdot 10^(-3) m^3)=60.4 J`

Answer 2

`W=60.4 J`

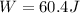
Work done is 60.4 Joules (J)

Step-by-step explanation:

Work done 'W' is given by:

`W=P\triangle V`

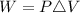
Where:

ΔV is the change in Volume.

P is the pressure.

Change in Volume=Final Volume-Initial Volume

Initial Volume= 127 mL

Final Volume= 654 mL

ΔV=654-127 (mL)

ΔV=527 mL

ΔV=0.527 L

Pressure Conversion:

1 atm=760 torr

`P=(860)/(760) \\P=1.1315\ atm`

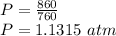
Now,

`W=P\triangle V`

`W=1.1315\ atm*0.527\ L`

`W=0.5963 L.atm`

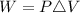
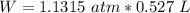
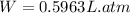
In joule (J): (Conversion 1 atm. L=101.325 J)

`W=0.5963\ L.atm*(101.325 J)/(1\ L.atm)`

`W=60.4 J`

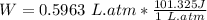
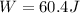
Work done is 60.4 Joules (J)