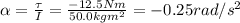Question

A child is riding a merry-go-round that has an instantaneous angular speed of 12 rpm. If a constant friction torque of 12.5 Nm is applied to the merry-go-round with a moment of inertia of 50.0 kg m2, what is the angular acceleration in rad/s2?

Answer 1

`-0.25 rad/s^2`

Step-by-step explanation:

The equivalent of Newton's second law for rotational motions is:

`\tau = I \alpha`

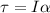
where

`\tau` is the net torque applied to the object

I is the moment of inertia

`\alpha` is the angular acceleration

In this problem we have:

`\tau = -12.5 Nm` (net torque, with a negative sign since it is a friction torque, so it acts in the opposite direction as the motion)

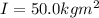`I=50.0 kg m^2` is the moment of inertia

Solving for
`\alpha`, we find the angular acceleration:

`\alpha = (\tau)/(I)=(-12.5 Nm)/(50.0 kg m^2)=-0.25 rad/s^2`