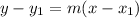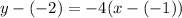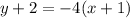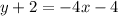Question

What is the equation in slope intercept form of the perpendicular bisector of the given line segment?

Answer 1

Explanation:

y = -4x - 6

Answer 2

y = -4x - 6

Explanation:

The equation of a line in point-slope form.

`y - y_1 = m(x - x_1)`

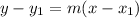
is the equation of the line containing point (x1, y1) and having slope, m.

The given point of the perpendicular bisector is (-1, -2), so in this case, x1 = -1, and y1 = -2.

We need the slope of the perpendicular bisector. First we find the slope of the segment. We start at point (-5, -3). We go up 1 unit and 4 units to the right, and we are at another point on the segment. Since slope = rise/run, the slope of the segment is 1/4. The slopes of perpendicular lines are negative reciprocals, so the slope of the perpendicular bisector is the negative reciprocal of 1/4, so for the perpendicular bisector, m = -4.

Now we use the equation above and our values.

`y - y_1 = m(x - x_1)`

`y - (-2) = -4(x - (-1))`

`y + 2 = -4(x + 1)`

`y + 2 = -4x - 4`

`y = -4x - 6`