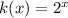Answer:
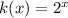 ⇒ 1st answer
⇒ 1st answer
Explanation:
* Lets explain how to solve the problem
∵
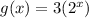
∵
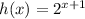
- Lets revise this rule to use it
# If
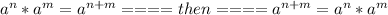
- We will use this rule in h(x)
∵
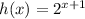
- Let a = 2 , n = x , m = 1
∴
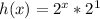
- Now lets find k(x)
∵ k(x) = (g - h)(x)
∵
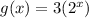
∵
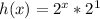
∴

- We have two terms with a common factor
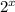
∵
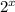 is a common factor
is a common factor
∵
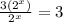
∵
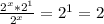
∴
![k(x) = 2^(x)[3 - 2]=2^(x)(1)=2^(x)](https://img.qammunity.org/2020/formulas/mathematics/college/y6r9pc4tnehzqjujckniy1c786m83bqtot.png)
*