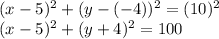Question

A circle is centered at the point (5, -4) and passes through the point (-3, 2).

The equation of this circle is (x + )2 + (y + )2 =
.
Reset

Answer 1

(x-5)^2+(y+4)^2=100

Explanation:

As we know the given points

Center = (5, -4)

and

Point on circle = (-3,2)

The distance between point on circle and center will give us the radius of circle

So,

The formula for distance is:

`\sqrt{(x_(2)-x_(1) )^(2)+(y_(2)-y_(1))^(2)}\\Taking\ center\ as\ point\ 1\ and\ the\ other\ point\ as\ point\ 2\\d=\sqrt{(-3-5)^(2)+(2-(-4))^(2)}\\d=\sqrt{(-8)^(2)+(2+4)^(2)}\\d=\sqrt{(-8)^(2)+(6)^(2)}\\\\d=√(64+36)\\d=√(100) \\ d=10\\So\ the\ radius\ is\ 10`

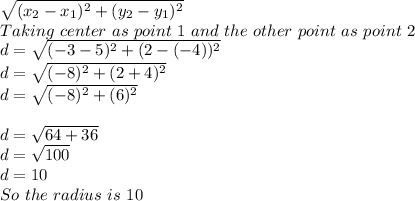
The standard form of equation of circle is:

`(x-h)^(2)+(y-k)^(2)=r^(2)`

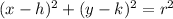
where h and k are the coordinates of the center. So putting in the value:

`(x-5)^(2)+(y-(-4))^(2)=(10)^(2)\\(x-5)^(2)+(y+4)^(2)=100`