Answer:
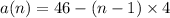
Explanation:
It's important to know that the graph is showing a linear function, which means its equation cannot be exponential. So, choices A and B are not correct here.
To find the correct equation, we could find the slope first with the following formula and the two given points
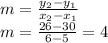
Now, we use the point-slope formula to find the equation
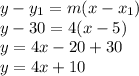
Notice that choice C has the same coefficient of 4, which is the slope of the line. Therefore, that's the right answer.
Let's prove it for
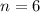
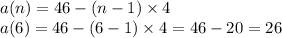
As the table shows.
Therefore, choice C is correct.