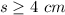Question

The function s(V) = describes the side length, in units, of a cube with a volume of V cubic units. Jason wants to build a cube with a minimum of 64 cubic centimeters.

What is a reasonable range for s, the side length, in centimeters, of Jason’s cube?

s > 0
s 4
s 8
s 16

Answer 1

`s\geq 4\ cm`

Explanation:

we know that

`s(V)=\sqrt[3]{V}`

where

s is the side length, in units, of a cube

V is the volume of a cube in cubic units

For a
`V=64\ cm^(3)`

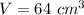
substitute in the formula

`s=\sqrt[3]{64}`

`s=4\ cms`

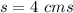
If Jason wants to build a cube with a minimum of 64 cubic centimeters

therefore

the minimum length side of the cube is 4 cm

`s\geq 4\ cm`