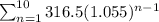Answer:
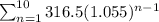
Explanation:
The amount (A) in a deposit after 1 year is calculated as follows:
A = P*(1 + r)
where:
P is the present value
r is the annual rate (decimal)
After the first year:
A = 300*(1 + 0.055) = $316.5
After the second year, the account will have a new amount of $316.5 due to the new $300 and the interest gained with the previous $316.5:
A = 316.5 + 316.5*(1 + 0.055)
After the third year:
A = 316.5 + [316.5 + 316.5*(1 + 0.055)]*(1 + 0.55)
A = 316.5 + 316.5*(1 + 0.055) + 316.5*(1 + 0.055)^2
After 10 years: