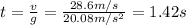Question

The equation for free fall at the surface of a celestial body in outer space​ (s in​ meters, t in​ seconds) is sequals10.04tsquared. How long does it take a rock falling from rest to reach a velocity of 28.6 StartFraction m Over sec EndFraction on this celestial body in outer​ space?

Answer 1

1.42 s

Step-by-step explanation:

The equation for free fall of an object starting from rest is generally written as

`s=(1)/(2)at^2`

where

s is the vertical distance covered

a is the acceleration due to gravity

t is the time

On this celestial body, the equation is

`s=10.04 t^2`

this means that

`(1)/(2)g = 10.04`

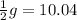
so the acceleration of gravity on the body is

`g=2\cdot 10.04 = 20.08 m/s^2`

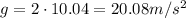
The velocity of an object in free fall starting from rest is given by

`v=gt`

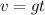
In this case,

g = 20.08 m/s^2

So the time taken to reach a velocity of

v = 28.6 m/s

is

`t=(v)/(g)=(28.6 m/s)/(20.08 m/s^2)=1.42 s`