Question

Please help!!! What is the decimal equivalent of this fraction? ​

Answer 1

`\bullet\ \ 0.\overline{15}`

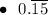
Explanation:

5/33 = (5·3)/(33·3) = 15/99 = 0.151515151515...

_____

You may recall that 1/9 = 0.11111...(repeating indefinitely). That is, a multiple of 1/9 is a single-digit repeating decimal.

Likewise, 1/99 = 0.01010101...(repeating indefinitely). This means when a 2-digit numerator has 99 as the denominator, the decimal equivalent is that number repeated indefinitely. Any fraction with 999 as the denominator is a 3-digit repeat in decimal; 9999 as the denominator gives a 4-digit repeat, and so on.