Prove by mathematical induction that 1+2+3+...+n= n(n+1)/2 please can someone help me with this ASAP. Thanks

Question

asked May 23, 2020 72.0k views

1 Answer

Clemesha · Answer 1 · 2020-05-30T13:54:18+0000

Let

$P(n):\ 1+2+\ldots+n = (n(n+1))/(2)$

In order to prove this by induction, we first need to prove the base case, i.e. prove that P(1) is true:

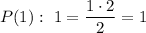
$P(1):\ 1 = (1\cdot 2)/(2)=1$

So, the base case is ok. Now, we need to assume
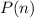P(n) and prove
P(n+1) .

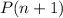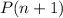P(n+1) states that

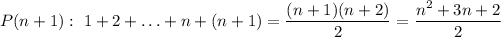
$P(n+1):\ 1+2+\ldots+n+(n+1) = ((n+1)(n+2))/(2)=(n^2+3n+2)/(2)$

Since we're assuming
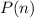P(n) , we can substitute the sum of the first n terms with their expression:

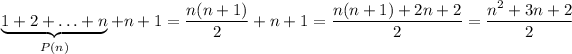
$\underbrace{1+2+\ldots+n}_(P(n))+n+1 = (n(n+1))/(2)+n+1=(n(n+1)+2n+2)/(2)=(n^2+3n+2)/(2)$

Which terminates the proof, since we showed that

$P(n+1):\ 1+2+\ldots+n+(n+1) =(n^2+3n+2)/(2)$

as required