Question

PLEASE HELP ME WITH THIS QUESTION ITS URGENT ITS ABOUT COMPLETING A EQUATION

Answer 1

(x - 2)² + (y +8)² = 49

Explanation:

Points to remember

Equation of a circle passing through the point (x₁, y₁) and radius r is given by

(x - x₁)² + (y - y₁)² = r ²

To find the radius

It is given that, center of circle = (-5, -8) and passes through the point (2 -8)

By using distance formula,

r = √[(2 --5)² + (-8 --8)²]

= √7²

r = 7

To find the equation of the circle

Here (x₁, y₁) = (2, -8)

Equation of circle is,

(x - x₁)² + (y - y₁)² = r ²

(x - 2)² + (y - (-8))² = 7²

(x - 2)² + (y +8)² = 49

Answer 2

The equation of circle is
`(x+5)^2+(y+8)^2=49`.

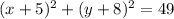Explanation:

The standard form of a circle is

`(x-h)^2+(y-k)^2=r^2` .... (1)

where, (h,k) is the center of the circle and r is the radius.

It is given that the center of the circle is (-5,-8). it means h=-5 and k=-8.

The circle passes through the point (2,-8). So, the radius of the circle is the distance between point (-5,-8) and (2,-8).

`r=√((x_2-x_1)^2+(y_2-y_1)^2)`

`r=√((2-(-5))^2+(-8-(-8))^2)`

`r=√(7^2+0)`

`r=7`

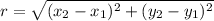
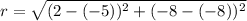
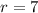
Substitute h=-5, k=8 and r=7 in equation (1), to find the equation of circle.

`(x-(-5))^2+(y-(08))^2=(7)^2`

`(x+5)^2+(y+8)^2=49`

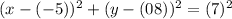
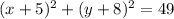
Therefore the equation of circle is
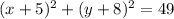`(x+5)^2+(y+8)^2=49`.