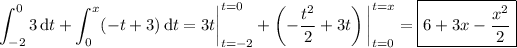1. The four subintervals are [0, 2], [2, 3], [3, 7], and [7, 8]. We construct trapezoids with "heights" equal to the lengths of each subinterval - 2, 1, 4, and 1, respectively - and the average of the corresponding "bases" equal to the average of the values of
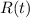 at the endpoints of each subinterval. The sum is then
at the endpoints of each subinterval. The sum is then
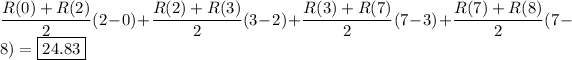
which is measured in units of gallons, hence representing the amount of water that flows into the tank.
2. Since
 is differentiable, the mean value theorem holds on any subinterval of its domain. Then for any interval
is differentiable, the mean value theorem holds on any subinterval of its domain. Then for any interval
![[a,b]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/x9eybysx3cihgn4xxsxk4fl3z5dcnyp7ww.png) , it guarantees the existence of some
, it guarantees the existence of some
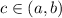 such that
such that
![\frac{R(b)-R(a)}{b-a)=R'(c)]()
Computing the difference quotient over each subinterval above gives values of 0.275, 0.3, 0.3, and 0.26. But just because these values are non-zero doesn't guarantee that there is definitely no such
 for which
for which
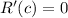 . I would chalk this up to not having enough information.
. I would chalk this up to not having enough information.
3.
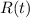 gives the rate of water flow, and
gives the rate of water flow, and
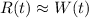 , so that the average rate of water flow over [0, 8] is the average value of
, so that the average rate of water flow over [0, 8] is the average value of
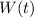 , given by the integral
, given by the integral
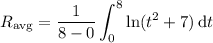
If doing this by hand, you can integrate by parts, setting

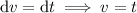
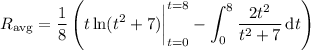
For the remaining integral, consider the trigonometric substitution
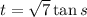 , so that
, so that
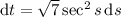 . Then
. Then
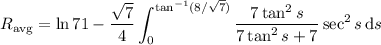
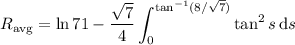
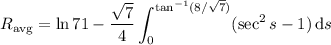
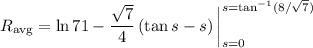
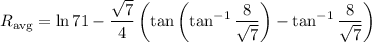

or approximately 3.0904, measured in gallons per hour (because this is the average value of
 ).
).
4. By the fundamental theorem of calculus,
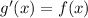
and
 is increasing whenever
is increasing whenever
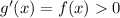 . This happens over the interval (-2, 3), since
. This happens over the interval (-2, 3), since
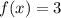 on [-2, 0), and
on [-2, 0), and
 on [0, 3).
on [0, 3).
5. First, by additivity of the definite integral,

Over the interval [-2, 0), we have
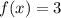 , and over the interval [0, 6],
, and over the interval [0, 6],
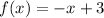 . So the integral above is
. So the integral above is