Question

Fit a quadratic function to these three points (-1, -11) (0,-3) and (3,-27)

Answer 1

`y = - 4 {x}^(2) + 4x - 3`

Step-by-step explanation

Let the quadratic function be

`y = a {x}^(2) + bx + c`

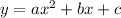
We substitute each point to find the constants, a,b, and c.

Substitute: (x=0,y=-3)

`- 3 = a {(0)}^(2) + b(0) + c`

`\implies \: c = - 3...(1)`

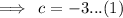
Substitute: (x=-1,y=-11) and c=-3

`- 11 = a {( - 1)}^(2) + b( - 1) + - 3`

`\implies \: - 11 = a - b - 3`

`\implies \: a - b = - 8...(2)`

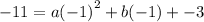
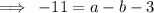
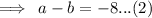
Substitute: (x=3,y=-27) and c=-3

`-27= a {( 3)}^(2) + b( 3) + - 3`

`\implies \: - 27 = 9a + 3b - 3`

`\implies \: 3a + b = - 8...(3)`

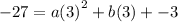
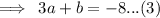
Add equations (3) and (2)

`3a + a = - 8 + - 8`

`4a = - 16`

`a = - 4`

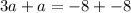
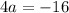
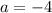
Put a=-4 in equation (2)

`- 4 - b = - 8`

`- b = - 8 + 4`

`- b = - 4`

`b = 4`

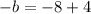
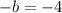
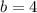
The quadratic equation is

`y = - 4 {x}^(2) + 4x - 3`