Question

the diagram show a closed structure in the shape of a half cylinder. the diameter of each base is 16 feet. the length of the structure is 50 feet. Find the surface area of the entire structure.

Answer 1

The surface area is
`SA=(800+464\pi)\ ft^(2)`

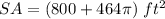
Explanation:

we know that

The surface area of the half cylinder is equal to

`SA=2B+PL`

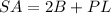
where

B is the area of the half circle

P is the perimeter of the half circle plus the diameter of circle

L is the length of the structure

Find the area B

The area of the half circle is

`B=(1)/(2) \pi r^(2)`

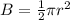
we have

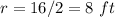`r=16/2=8\ ft` -----> the radius is half the diameter

substitute

`B=(1)/(2) \pi (8)^(2)`

`B=32\pi\ ft^(2)`

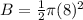
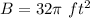
Find the value of P (the perimeter of the half circle plus the diameter of circle)

`P=\pi r+D`

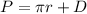
we have

`D=16\ ft`

`r=8\ ft`

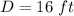
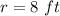
substitute

`P=\pi (8)+16`

`P=(8\pi+16)\ ft`

Find the surface area

`SA=2B+PL`

`L=50\ ft`

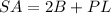
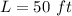
substitute

`SA=2(32\pi)+(8\pi+16)(50)`

`SA=64\pi+400\pi+800`

`SA=(800+464\pi)\ ft^(2)`

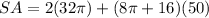
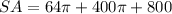
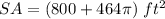
see the attached figure to better understand the problem