1. The four subintervals are [0, 2], [2, 5], [5, 6], and [6, 7]. Their respective right endpoints are 2, 5, 6, and 7. If
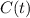 denotes the change in sea level
denotes the change in sea level
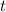 years after 2010, then the total sea level rise over the course of 2010 to 2017 is
years after 2010, then the total sea level rise over the course of 2010 to 2017 is
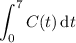
approximated by the Riemann sum,
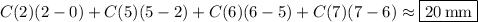
2. The sum represents the definite integral
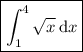
That is, we partition the interval [1, 4] into
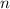 subintervals, each of width
subintervals, each of width
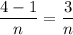 . Then we sample
. Then we sample
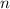 points in each subinterval, where
points in each subinterval, where
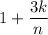 is the point used in the
is the point used in the
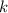 th subinterval, then take its square root.
th subinterval, then take its square root.
3. The integral is trivial:
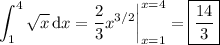
4. Using the fundamental properties of the definite integral, we have
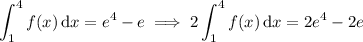
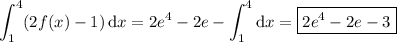
5. First note that
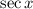 is undefined at
is undefined at
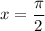 , so the integral is improper. Recall that
, so the integral is improper. Recall that
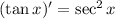 . Then
. Then
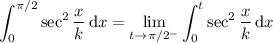
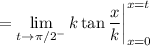
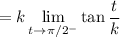
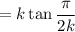
Now,
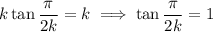
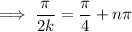
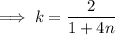
where
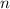 is any integer.
is any integer.