1. Let
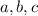 be the three points of intersection, i.e. the solutions to
be the three points of intersection, i.e. the solutions to
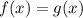 . They are approximately
. They are approximately
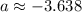
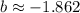
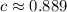
Then the area
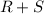 is
is
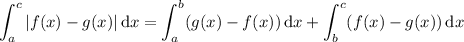
since over the interval
![[a,b]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/x9eybysx3cihgn4xxsxk4fl3z5dcnyp7ww.png) we have
we have
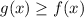 , and over the interval
, and over the interval
![[b,c]](https://img.qammunity.org/2020/formulas/mathematics/high-school/ts425uqaxpsaesi0137qe811xdggs9k2m4.png) we have
we have
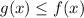 .
.
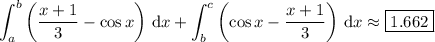
2. Using the washer method, we generate washers with inner radius
 and outer radius
and outer radius
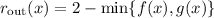 . Each washer has volume
. Each washer has volume
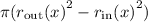 , so that the volume is given by the integral
, so that the volume is given by the integral
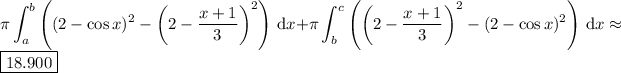
3. Each semicircular cross section has diameter
 . The area of a semicircle with diameter
. The area of a semicircle with diameter
 is
is
 , so the volume is
, so the volume is
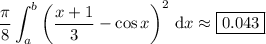
4.
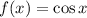 is continuous and differentiable everywhere, so the the mean value theorem applies. We have
is continuous and differentiable everywhere, so the the mean value theorem applies. We have
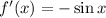
and by the MVT there is at least one
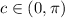 such that
such that
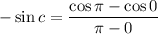
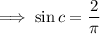
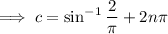
for integers
 , but only one solution falls in the interval
, but only one solution falls in the interval
![[0,\pi]](https://img.qammunity.org/2020/formulas/mathematics/high-school/ff7ej2jpk0i4kn6n9i43ftibbox6kl9dqz.png) when
when
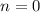 , giving
, giving
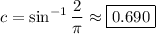
5. Take the derivative of the velocity function:
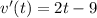
We have
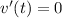 when
when
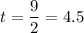 . For
. For
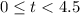 , we see that
, we see that
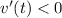 , while for
, while for
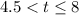 , we see that
, we see that
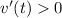 . So the particle is speeding up on the interval
. So the particle is speeding up on the interval
 and slowing down on the interval
and slowing down on the interval
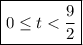 .
.