Answer:
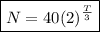
Explanation:
The growth of bacteria is an exponential function. The equation has the general form
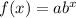
Using the variables N and T, we can rewrite the equation as
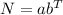
We have two conditions:
(1) There are 40 bacteria at T = 0
(2) There are 80 bacteria at T = 3.
Insert these values into the equation.
