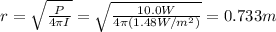Question

Suppose the maximum safe intensity of microwaves for human exposure is taken to be 1.48~\mathrm{Watts/m^2}1.48 Watts/m ​2 ​​ . If a radar unit leaks 10.0~\text{Watts}10.0 Watts of microwaves (other than those sent by its antenna) uniformly in all directions, how far away must you be to be exposed to an intensity considered to be safe? Recall that Watts = Joules/second = power = energy per unit time. Assume that the power of the electromagnetic waves spreads uniformly in all directions (i.e. spreads out over the area of a sphere) and use the formula for the surface area of a sphere.

Answer 1

0.733 m

Step-by-step explanation:

The maximum safe intensity for human exposure is

`I= 1.48 W/m^2`

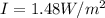
Intensity is defined as the ratio between the power P and the surface irradiated A:

`I=(P)/(A)`

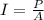
For a source emitting uniformly in all directions, the area is the surface of a sphere of radius r:

`A=4 \pi r^2`

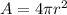
So

`I=(P)/(4\pi r^2)`

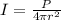
In this case, we have a radar unit with a power of

P = 10.0 W

So we can solve the previous equation to find r, which is the distance at which a person could be considered to be safe:

`r=\sqrt{(P)/(4\pi I)}=\sqrt{(10.0 W)/(4 \pi (1.48 W/m^2))}=0.733 m`