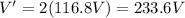Question

Two large parallel conducting plates carrying opposite charges of equal magnitude are separated by 2.20 cm.?(a)If the surface charge density for each plate has magnitude 47.0 nC/m2, what is the magnitude of E_field in the region between the plates? (b)What is the potential difference between the two plates? (c)If the separation between the plates is doubled while the surface charge density is kept constant at the value in part (a), what happens to the magnitude of the electric field? (d)If the separation between the plates is doubled while the surface charge density is kept constant at the value in part (a), what happens to the potential difference?

Answer 1

The electric field between the plates is 5.31 x 10^3 N/C, and the potential difference is 116.82 V. Doubling the separation distance between the plates keeps the electric field the same, but doubles the potential difference.

Step-by-step explanation:

For two large parallel conducting plates carrying opposite charges of equal magnitude separated by 2.20 cm with a surface charge density of 47.0 nC/m2, the magnitude of the electric field (Enfield) between the plates can be found using the formula E = σ / ε0, where σ is the surface charge density and ε0 is the permittivity of free space. Plugging the given values in, we find:
E = (47.0 × 10-9 C/m2) / (8.85 × 10-12 C2/N·m2)
= 5.31 × 103 N/C

The potential difference (V) between the plates is given by V = E × d, where d is the separation between the plates. Therefore:

V = (5.31 × 103 N/C) × (0.022 m)
= 116.82 V

If the separation between the plates is doubled while keeping the surface charge density constant, the magnitude of the electric field remains the same because it is dependent only on surface charge density, not distance. However, the potential difference will double because it is a product of electric field strength and the separation distance.

Answer 2

(a) 5310.7 V/m

The magnitude of the electric field between two parallel plates is given by

`E=(\sigma)/(\epsilon_0)`

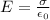
where

`\sigma` is the surface charge density

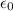`\epsilon_0` is the vacuum permittivity

In this problem,

`\sigma = 47.0 nC/m^2 = 47.0 \cdot 10^(-9) C/m^2`

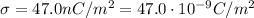
So the electric field here is

`E=(47.0\cdot 10^(-9) C/m^2)/(8.85\cdot 10^(-12)F/m)=5310.7 V/m`

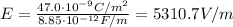
(b) 116.8 V

The potential difference between the two plates is given by

`V= Ed`

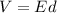
where

E is the magnitude of the electric field

d is the separation between the plates

Here we have

E = 5310.7 V/m

d = 2.20 cm = 0.022 m

So the potential difference is

`V=(5310.7 V/m)(0.022m)=116.8 V`

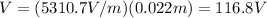
(c) The electric field does not change

Step-by-step explanation:

As stated in part (a), the magnitude of the electric field is given by

`E=(\sigma)/(\epsilon_0)`

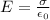
where

`\sigma` is the surface charge density

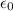`\epsilon_0` is the vacuum permittivity

as we can see, the value of E depends only on the surface charge density, which is kept constant in this case, so the value of the electric field strength does not change.

(d) The potential difference doubles (233.6 V)

In this situation, the separation between the plates is doubled, so:

d' = 2 d

The potential difference depends linearly on the separation between the plates:

V = Ed

where

E is the magnitude of the electric field (which is kept constant)

d is the separation between the plates

So the new potential difference will be

`V' = E(2d) = 2 (Ed) = 2 V`

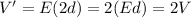
which means that the potential difference will double:

`V'=2 (116.8 V)=233.6 V`