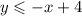Question

Write the linear Inequality shown in the graph. The gray area represents the shaded region.

Answer 1

`y \leqslant - x + 4`

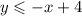
EXPLANATION

The equation of the boundary line is

`y = - x + 4`

Hence the inequality is either

`y \leqslant - x + 4`

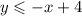
or

`y \geqslant - x + 4`

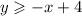
We test the origin to get determine which one represents the shaded

We substitute (0,0) into the first inequality to get;

`0\leqslant - (0) + 4`

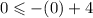
This implies that,

`0 \leqslant 4`

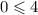
Hence the correct answer is

`y \leqslant - x + 4`

Answer 2

Answer: Second Option

`y \leq -x +4`

Explanation:

The region is bounded by a line of negative slope that cuts the y-axis at the point y = 4 and cuts the x-axis at the point x = 4.

So the equation of this line is

`y = -x + 4`

If the region is composed of all the points that lie below the line y = -x + 4 then it means that the region is formed by all the values of y less than or equal to the line
`-x + 4`.

Therefore the inequation is:

`y \leq -x +4`

Second Option