Question

You want to calculate the value of your car each year when it depreciates by 15%. What does the term y mean in the exponential function y=9500*0.85^x?

Answer 1

the value of your car after x years

Explanation:

The given function represents a geometric sequence with initial term $9500 and common factor 0.85. Note that every time x increases by 1, we get the newest term by multiplying the previous one by 0.85. The given function y=9500*0.85^x represents the value of your car after x years (which matches the 3rd answer choice).

Answer 2

Value of the car after x years

Explanation:

Exponential functions are generally expressed in the form:
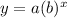`y=a(b)^x` and since this function is decreasing, meaning it has an exponential decay, it can be expressed as:
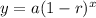`y=a(1-r)^x` where r=rate of decay.

In this case the a represents the initial value or y-intercept, since when x=0, (1-r)^0 = 1, so we just have y=a(1) or y=a

The r represents the rate of decay

the x usually represents the time in seconds, days, months, or whatever unit is being used

The y value represents the value of whatever your measuring, and in this context it represents the value of the car after x years.

This is because a represents the initial value

After one year it's only 85% worth it's initial value or 15% less which is represented as 0.85(a)

After two years it's only 85% worth the previous year or 15% less the previous year, which is represented as 0.85(0.85(a))

This will continue to decrease the number of years increase