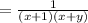Answer:
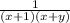
Explanation:
Given the expression:
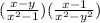
The first step is to multiply the numerator of the first fraction by the numerator of the second fraction and the denominator of the first fraction by the denominator of the second fraction. Then:
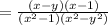
Since
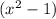 and
and
 are perfect squares, you can factorize them in the form:
are perfect squares, you can factorize them in the form:
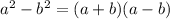
Then:
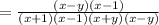
Simplifying, you get: